So when I posted on Facebook about the peculiar phenomenon of the Thue-Morse sequence making snowflake curves, Owen immediately asked the logical question: what about those fancier sequences associated with his recursively nested three-legged or n-legged multifractions? The n-ary Thue-Morse sequences, as I'm calling them? What do they do when you let the same turtle algorithms loose on them?
Well, I tried it and immediately got these nice things. This is the ternary Thue-Morse sequence interpreted with a 1 as "move forward and turn left 60 degrees", anything else as "move forward and turn right 60 degrees":
And this is the same thing with 1 as "move forward" and anything else meaning "turn left 30 degrees":

These ternary ones look a little like the Lévy C fractal, only different.
They're differently oriented but you can see they have the same vertically-stretched appearance. That's real: I left in the numbered axes so you can see the picture hasn't just been displayed at the wrong aspect ratio. That's weird, to me--there's nothing about my drawing rules that singles out a special direction in the plane (aside from the initial condition). It must be something about the long-range internal correlations in the sequence itself.
Much as with the binary Thue-Morse sequence, you can get a fractal of this appearance in a lot of ways out of this sequence.
You'll notice, though, that I'm dropping some information here: for both of these curves, I'm paying attention to whether a digit is a 1 or not, but not to the difference between 0 and 2. If, instead, the digit 2 is singled out, I get this (here 2 means "move forward" and anything else is "turn left 90 degrees":

Weird, now the stretching is horizontal. (Also I ran it on much more of the sequence so you can see more of the fractal structure.) But it's not magically fated to look like this no matter what--if I assign different actions to all three digits, then I can get out some completely different-looking fractals, like this one-- this is "1=move forward, 2=turn left 45 degrees, 0=turn left 90 degrees":

And sometimes the symmetries in the sequence cause any fractal structure to collapse out altogether--if you use the "move forward/turn left 60 degrees" rule on this one, for instance, you don't get a fractal, it just traces over and over this shape that reminds me of an Autobot face:
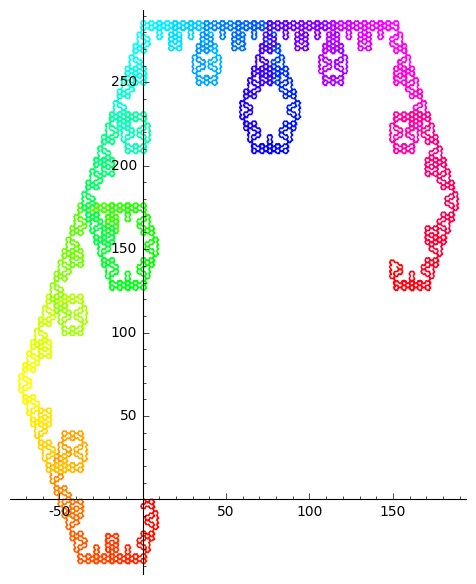
The higher n-ary Thue-Morse sequences similarly converge on these sort of squashed cauliflowery looking shapes. Singling out one digit as special seems to produce more and more squashing/stretching the higher you go. Here's a base-5 one:

Well, I tried it and immediately got these nice things. This is the ternary Thue-Morse sequence interpreted with a 1 as "move forward and turn left 60 degrees", anything else as "move forward and turn right 60 degrees":

And this is the same thing with 1 as "move forward" and anything else meaning "turn left 30 degrees":

These ternary ones look a little like the Lévy C fractal, only different.
They're differently oriented but you can see they have the same vertically-stretched appearance. That's real: I left in the numbered axes so you can see the picture hasn't just been displayed at the wrong aspect ratio. That's weird, to me--there's nothing about my drawing rules that singles out a special direction in the plane (aside from the initial condition). It must be something about the long-range internal correlations in the sequence itself.
Much as with the binary Thue-Morse sequence, you can get a fractal of this appearance in a lot of ways out of this sequence.
You'll notice, though, that I'm dropping some information here: for both of these curves, I'm paying attention to whether a digit is a 1 or not, but not to the difference between 0 and 2. If, instead, the digit 2 is singled out, I get this (here 2 means "move forward" and anything else is "turn left 90 degrees":

Weird, now the stretching is horizontal. (Also I ran it on much more of the sequence so you can see more of the fractal structure.) But it's not magically fated to look like this no matter what--if I assign different actions to all three digits, then I can get out some completely different-looking fractals, like this one-- this is "1=move forward, 2=turn left 45 degrees, 0=turn left 90 degrees":

And sometimes the symmetries in the sequence cause any fractal structure to collapse out altogether--if you use the "move forward/turn left 60 degrees" rule on this one, for instance, you don't get a fractal, it just traces over and over this shape that reminds me of an Autobot face:

The higher n-ary Thue-Morse sequences similarly converge on these sort of squashed cauliflowery looking shapes. Singling out one digit as special seems to produce more and more squashing/stretching the higher you go. Here's a base-5 one:
